پروژه بهینه سازی کارایی سیستم بلادرنگ با محدودیت توابع زمان/بهره وری


دسته : سمینار کامپیوتر
فرمت فایل : word
حجم فایل : 1607 KB
تعداد صفحات : 10
بازدیدها : 9401
برچسبها : بهینه سازی کارایی سیستم بلادرنگ
مبلغ : 10900 تومان
خرید این فایلدانلود ترجمه مقاله گزارش سمینار فناوری اطلاعات، بهینه سازی کارایی مبتنی بر مدل تحلیلی در سیستم های بلادرنگ با محدودیت توابع زمان و بهره وری
دانلود ترجمه مقاله گزارش سمینار کارشناسی ارشدرشته مهندسی فناوری اطلاعات گرایش شبکه های کامپیوتری - پروژه بهینه سازی کارایی مبتنی بر مدل تحلیلی در سیستم های بلادرنگ با محدودیت توابع زمان / بهره وری
Performance Optimization Based on Analytical Modeling in a Real-Time System with Constrained Time/Utility Functions
مقدمه
در این مقاله به بیان چهار معیار برای ارزیابی کارایی در یک سیستم بلادرنگ firm پرداخته شده است. تمامی این معیارها بر اساس بهره وری سیستم هستند. سپس با استفاده از روش های تحلیلی به محاسبه این معیارها پرداخته شده و در نهایت نیز توسط روش های عددی یک بهینه سازی برای آن ها ارائه شده است.
به طور کلی سیستم های بلادرنگ را می توان به سه دسته بلادرنگ سخت، بلادرنگ نرم و بلادرنگ firm تقسیم کرد. مسئله اساسی در سیستم های بلادرنگ سخت، موضوع برآورده شدن ضرب العجل ها می باشد، در حالی که در سیستم های بلادرنگ نرم و بلادرنگ firm فقط مسئله تمام شدن کارها قبل از فرا رسیدن ضرب العجل مطرح نیست، بلکه این که اجرای کار ها دقیقا در چه زمانی به اتمام می رسد نیز مهم است. اثر این موضوع را معمولا توسط توابع بهره وری یا TUF ها وارد مسئله می کنند.
TUF ها انواع مختلفی دارند، به طور مثال می توانند به صورت پله ای و یا غیر پله ای باشند و یا حالت صعودی یا نزولی داشته باشند، اما به طور کلی این توابع را می توان به دو دسته Unimodal و Multimodal تقسیم کرد. در انواع Unimodal اگر تابع بهره وری در یک لحظه به صورت نزولی شود، پس از آن دیگر نمی تواند حالت صعودی پیدا کند، به عبارت دیگر هر گونه کاهش در مقدار بهره وری نمی تواند با یک افزایش دنبال شود. اما در انواع Multimodal چنین محدودیتی نداریم. نکته دیگری که در مورد TUF ها وجود دارد این است که در اکثر بحث های مربوط به بهره وری معمولا هدف بیشینه کردن تابع TUF است و یا تضمین اینکه میزان این تابع از یک حداقل مقداری کمتر نشود. در معیار های کارایی مطرح شده در این مقاله هر دوی این موارد لحاظ شده است.
محاسبه چهار معیار کارایی مطرح شده
پس از تعریف معیارهای کارایی سعی می شود با استفاده از روش های تحلیلی به محاسبه این معیارها پرداخته شود. توابعU(τ,θ) و G(t) به عنوان داده های مسئله در نظر گرفته می شوند. بنابراین تنها مجهول باقی مانده در فرمول سه معیار fv(τ) است. برای محاسبه fv(τ) آن را بر حسب حالات سیستم یعنی تعداد کارهای سیستم در هر لحظه تعریف می کنیم:
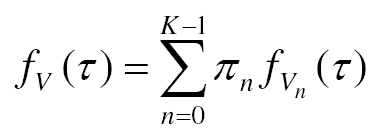
که تابع fv(τ) تابع PDF متغیر تصادفی Vn (زمان اقامت برای حالتی که n کار در سیستم باشند) است. πn نیز احتمال اینکه n کار در سیستم باشند را مشخص می کند.
سمینار بهینه سازی کارایی مبتنی بر مدل تحلیلی در سیستم های بلادرنگ با محدودیت توابع زمان/بهره وری
فهرست
مقدمه
معیارهای کارایی
مدل سیستم
معیارهای کارایی
محاسبه چهار معیار کارایی مطرح شده
بهینه کردن معیار های کارایی مطرح شده
ارزیابی های تجربی
نتیجه گیری
ویژگی های مقاله
ادامه کار
خرید و دانلود آنی فایل